|
MODULE No 4 |
|
Titre :
Introduction à |
|
But : Permettre aux étudiants de passer de phrases « simples » de la langue française à des diagrammes statiques montrant les concepts (classes) du domaine et des associations simples. (modèles conceptuels en UML) |
|
Antécédents : Module 2. |
|
Corps : Note Dans le cadre de ce cours nous allons employer souvent de manière interchangeable les termes « classe » et « concept ». Vous avez déjà des idées très claires sur ce qu’est une classe, en ce qui concerne ce qu’est un concept vous en avez une certaine vision intuiticve. Selon le TLF un concept est « Une représentation abstraite et générale, objective, stable, munie s’un support verbal. […] Synomyme : Classe […] ». Fin de la note. Le schéma UML suivant est une représentation statique (le temps
n’est pas représenté) de votre outil principal de travail :
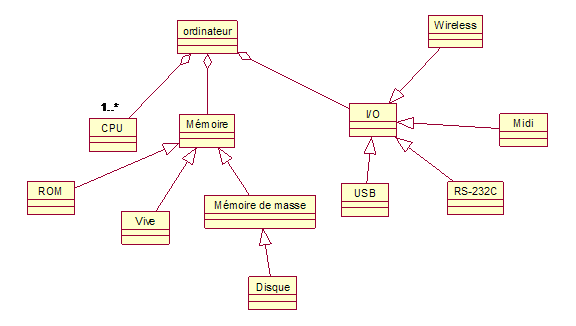
l’ordinateur. Le schéma est une « Diagramme de classe » ou
« Diagramme conceptuel » représenté avec Un ordinateur est constitué de (ou est un agrégat de) un ou plusieurs CPU, de la Mémoire et de I/O. ROM, Vive, Mémoire de masse sont des Mémoire. Un disque est de type Mémoire de masse. Wireless,
Midi, RS-
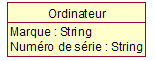
Une boîte rectangulaire représente un concept (classe). Le nom du concept (classe) apparaît dans la boîte (dans la figure précédente, ordinateur, CPU, Mémoire… sont les concepts). Dans le schéma précédent rien n’est dit sur les attributs de l’ordinateur. La seule chose qu’on connait ce sont les concepts (classes) auxquels il est associé. Si on voulait définir des attributs de l’ordinateur on pourrait par exemple choisir : · Marque · Numéro de série La représentation graphique en UML de l’ordinateur avec ses deux attributs serait la suivante :
Note
Comme vous l’avez appris dans vous cours de programmation il ne faut pas
confondre une classe (concept) avec une instance de Les boîtes (les concepts) peuvent être reliées par une ligne qui
représente une association. Une association étant une relation entre les
concepts. Attention : Dans Les rectangles avec un coin retourné sont des commentaires. Note Une association
entre deux concepts est dite binaire. Il s’agit de l’association la plus
simple à comprendre et donc la plus employée en analyse. Une association
entre n concepts est dite n-aire. Fin
de Dans la figure précédente les concepts sont reliés entre eux avec deux associations spéciales : l’une ayant à l’origine un triangle et l’autre un losange. Le triangle à la fin d’une association est une notation pour indiquer que la boîte (le concept) touché par le triangle est une généralisation du concept à l’autre bout de la ligne (L’association est donc une généralisation). Le triangle peut donc être considéré comme la « traduction » en UML du français « est un » (« Is a » en anglais). Le losange à la fin d’une association est une notation pour indiquer que le concept touché par le losange est un agrégat des parties à l’autre bout de l’association. Le losange peut donc être considéré comme la « traduction » en UML du français « est constitué de » ou « est un agrégat de ». Généralisation (« est un ») Mais, qu’est-ce qu’une généralisation ? Une généralisation
est une relation de type classificatoire (taxonomique) entre deux concepts.
Le concept moins général (celui qui est plus spécialisé) a toutes les
caractéristiques (ou attributs comme on dit en UML et en GL lorsque l’on
parle d’une classe) du concept plus général avec des ajouts ou des
limitations : le concept plus spécialisé doit être cohérent avec celui
qui est plus général et ne doit pas « perdre » des caractéristiques
(des attributs). La relation de généralisation permet de partager des caractéristiques,
d’en ajouter : les concepts sont différents tout en ayant des
similitudes, Les caractéristiques partagées permettent « une économie » de pensée. On dite que le concept spécialisé hérite
les caractéristiques du concept général. Si un mammifère est un vertébré et si les vertébrés sont caractérisés par des vertèbres osseuses alors les mammifères doivent avoir des vertèbres osseuses. Les mammifères sont une spécialisation des vertébrés et dans leur spécialisation ils ajoutent, entre autres, le fait qu’ils sont dotés de mamelles, qu’ils ont un cœur avec quatre cavités, etc.
Un homo sapiens sapiens est un mammifère : la relation de généralisation est transitive : Si A est un B et B est un C alors A est un C. On appelle discriminateur la caractéristique qui permet la généralisation : la parole, par exemple, discrimine les Bonobo des homo sapiens sapiens. Un discriminateur est de type énumération (dans le cas que nous venons de citer il s’agit d’une énumération spéciale : vrai et faux, de booléen) Dans la spécialisation on n’est pas « limité » aux ajouts. On peut aussi restreindre. S’il est vrai que l’éléphant et la souris sont des mammifères et que les femelles produisent du lait, il est aussi clair que si l’on fixe une « quantité maximale de lait pour les mammifères femelles » (celle des baleines par exemple) alors le concept « éléphant » force une diminution de la quantité maximale et le concept de « souris » le diminue encore plus ! Note : les mammifères ne sont pas des animaux que produisent du
lait : seules les femelles en produisent. Mammifère est un mot d’origine
latine qui signifie « porteur de mamelles ». Fin de Quelle est l’utilité des généralisations ? La généralisation permet d’organiser les concepts dans une hiérarchie où chaque position dans la hiérarchie permet d’oublier ce qu’il y a en dessous, de considérer comme acquis ce qu’il y a en dessus et de se concentrer au niveau auquel on se situe. Si on considère la figure précédente et on suppose d’être en train de considérer le concept de « primate » on peut considérer que tout ce qui concerne le lait est « réglé » dans le concept de « mammifère » et que ce qui concerne l’écriture est un « détail » qui concerne le concept plus détaille de « homo sapiens sapiens ». La généralisation permet donc une grande économie conceptuelle. Elle facilite aussi la recherche des différence à un même niveau de la hiérarchie : entre bonobo et homo sapiens sapiens, par exemple. Quel est le danger des
généralisations ? De rendre rigide et lourde
Note pour les programmeurs, s’il
y a en a parmi les lecteurs. Des hiérarchies
profondes dans le sous-classage rendent souvent lourde l’application,
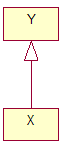
difficile la réutilisation et donc coûteux l’entretien Fin de Quand généraliser ? Toutes les fois que l’on s’aperçoit que le concept général aide dans la compréhension du domaine, qu’il a une certaine autonomie et qu’il est employé par d’autres personnes. Donc toutes les fois que vous dites x est un y vous pouvez le représenter comme suit :
Mais alors, si je dis que « Jean est un homme », puis-je le décrire avec
NON !!!! Non, parce que Jean n’est pas un concept mais un individu. Dans notre jargon on dit que Jean est une instance de Homo sapiens sapiens. Dit d’une autre manière Homo sapiens sapiens est une classe et Jean une instance de la classe. En UML un objet (un individu ou une instance) est représenté comme suit :
Peut-on donc représenter l’association entre Homme et Jean de la manière suivante ?
Encore une fois NON !!!! Pour les mêmes considérations qu’auparavant, même si cette fois Par contre on peut représenter le fait que Jean est fils de Sylvie comme suit :
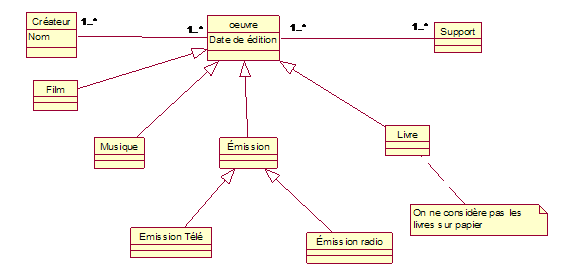
Attention : le monde « réel » dans la figure précédente n’est pas vraiment le monde réel mais une représentation photographique, Quelqu’un qui connaît Sylvie pourrait la reconnaître dans la photo et dire que c’est bien la Sylvie qui est mère de Jean. Il faut bien sûr que l’enfant de la photo soit le Jean qui est fils de Sylvie ! Et s’il a mal reconnu ? Voilà le genre de problèmes qui, souvent, n’est pas facile à résoudre. Comme on l’a déjà dit le monde est enveloppé dans le langage (et dans les images aussi). Pour compliquer encore plus les choses on pourrait imaginer que la femme s’appelle Sylvie mais n’est pas la Sylvie à laquelle nous pensions (celle de notre application). C’est pour cela que le nom (et surtout le prénom) ne suffit pas pour identifier de manière univoque un objet, comme tout le monde sait. Voici un autre diagramme conceptuel pour décrire les différents types d’œuvres (TP de l’été 2006).
Qu’est-ce que la « date de création »? Une
caractéristique (attribut). Pour suivre Mais la date n’est-elle pas un concept ?
Bien sur que oui (tout nom commun est un concept). Pour qu’un nom commun
devienne un objet (objet dans le sens où nous l’employons) il faut qu’on
ajoute, par exemple, « ce…. –ci » : Cette date-ci. Que l’on
indique parmi l’ensemble de date une date spécifique : la date de
naissance de Joyce, la date de notre rencontre, la date de l’examen de INF
5151, etc. Pourquoi dans notre exemple la date n’est-elle
pas représentée comme concept ? Parce que l’on juge que pour les
objectifs de notre projet la date n’a pas d’autonomie : elle n’évolue
pas indépendamment de Œuvre et puis elle est un « type » simple.
Mettre la date comme attribut facilite la mise en œuvre même si elle pourrait
compliquer la maintenance. Note Le choix de représenter un élément
comme attribut de la classe ou comme une classe autonome est souvent loin
d’être banal. Seul le contexte et les objectifs de qualité permettent de
faire des choix éclairés. Fin de la
note Agrégation (« est constitué
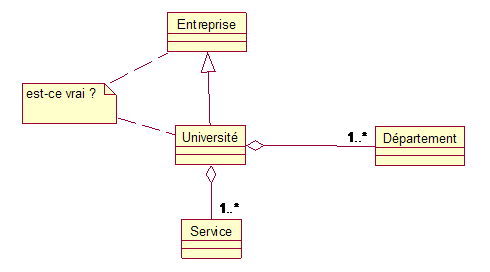
de ») L’agrégation est une association entre concepts qui sont dans une relation de tout à partie. Voici un autre exemple d’emploi de l’agrégation : une université est constituée de un ou plusieurs département et de un ou plusieurs service
Association On a vu deux types particuliers d’association et ceci devrait nous permettre d’apprendre plus facilement ce qu’est une association (souvent le travail de l’élément moins général à l’élément plus général est plus facile que le contraire). Mais qu’est-ce qu’une association ? Qu’est-ce que le concept qui généralise « généralisation » et « agrégation » ? Prenons la définition du manuel de UML (légèrement modifiée pour l’adapter au cours) : « Une association est une relation entre deux ou plusieurs classes qui décrit les connections entre leurs instances. (…) Chaque instance d’une association qui s’appelle lien (link en anglais) est une liste ordonnée de références à des objets. (…) Une association a un nom optionnel. (…) Chaque fin d’association a un rôle et une multiplicité qui indique combien de fois un objet peut apparaître dans les liens dans l’association ». Les associations, comme les liens, apparaissent souvent dans les description en langue naturelle comme des verbes : les professeurs enseignent dans les universités. Enseigne est l’association entre le concept de professeur et celui d’université. Marc enseigne à l’UQAM, Jean enseigne à McGill, François enseigne à Harvard sont trois liens entre trois couples d’objets qui sont des instances de professeur et d’université. |
|
Conséquents :
· Connaître les rudiments de UML · Concept (classe) et objet · Association et lien · Attribut · Généralisation et agrégation |
|
Note
01 : |